수학과 예술의 결합은 오랫동안 많은 창작자들에게 영감을 주어왔습니다. 특히 AI 이미지 생성 도구가 발전하면서 수학적 함수와 개념을 시각화하는 새로운 방법이 등장했습니다. 이번 글에서는 최신 미드저니 V7 알파를 활용해 수학적 아트를 만드는 과정과 그 매력에 대해 알아보겠습니다.

생성형 아트의 진화: 수학에서 AI까지

생성형 아트(Generative Art)라는 개념은 미드저니 같은 AI 도구가 등장하기 훨씬 전부터 존재했습니다. 전통적인 생성형 아트에서 창작자는 붓이나 조각 도구 대신 시스템으로 시작합니다. 여기서 시스템이란 규칙, 방정식, 또는 코드의 집합을 의미합니다. 이 시스템에서 무한한 변형이 펼쳐질 수 있으며, 각각은 수학적 가능성의 독특한 산물입니다.

3D 아티스트들에게 이 방법은 새로운 형태의 창의성을 열어주었습니다. 수작업으로 형태를 만드는 대신 그 형태가 나타날 수 있는 조건을 정의함으로써 작품을 구성할 수 있게 되었습니다. 생성적 방법은 복잡성을 탄생시키는 도구가 되었습니다:

• 유기적으로 느껴지는 지형
• 물리 법칙을 뛰어넘는 건축물
• 생명체처럼 진화하는 구조물

아티스트는 모든 능선이나 꼭짓점을 모델링하는 대신, 성장, 대칭, 노이즈 또는 재귀의 논리를 구축하고 형태가 스스로 생성되도록 합니다.

프랙탈에서 다양한 수학 함수로

3D 생성형 아트는 프랙탈을 대중화시키고 프랙탈 아트라는 새로운 움직임을 탄생시켰습니다. 수학, 코드, 고급 렌더링 엔진의 조합을 통해 셀 수 없이 많은 놀라운 이미지들이 만들어졌습니다.

프랙탈은 이제 친숙한 용어가 되었지만, 수학은 더 많은 아름다운 것들을 제공합니다. 다양한 수학 함수의 기하학적 표현이 많이 존재하며, 각각은 독특하고 특별하며, 수학적이면서도 약간 예측할 수 없는 요소를 가지고 있습니다.

미드저니와 수학적 아트의 만남

미드저니는 직접적으로 수학을 이해하거나 수학 함수를 정확하게 해석할 수는 없지만, 학습 과정에서 수학적 그래프, 함수 플롯, 그리고 3D 아티스트들이 만든 생성형 아트를 접했습니다. 이런 배경 지식을 바탕으로 미드저니 V.6에서도 이미 훌륭한 수학 이미지를 만들 수 있었습니다.

프랙탈, 이상한 끌개(strange attractors), 그리고 다른 많은 함수들은 정확하지는 않더라도 미드저니가 환상적인 이미지를 만드는 데 도움이 되었습니다. 또한 이러한 수학적 이미지를 기반으로 한 무드보드를 만들어 미드저니 V.6에서 새롭고 흥미로운 스타일을 만드는 데 활용했습니다.

미드저니 V7 로 수학적 아트 만들기

최신 버전인 미드저니 V7 알파는 수학적 아트 생성에 어떤 성능을 보여줄까요? 테스트를 위해 매우 간단한 프롬프트를 사용했습니다:

“Abstract mathematical art, [함수 이름], shallow focus, bokeh.”

이 프롬프트와 함께 다음과 같은 흥미로운 수학 함수들을 활용했습니다:

테스트에 사용된 수학 함수 목록

1. 벤 다이어그램(Venn Diagrams): 집합 관계를 시각화하는 고전적인 방법
2. 오일러 다이어그램(Euler Diagrams): 벤 다이어그램의 일반화
3. 보로미안 링(Borromean Rings): 세 개의 링이 두 개씩은 연결되지 않지만 세 개가 분리될 수 없는 특별한 구조
4. 베르누이의 렘니스케이트(Lemniscate of Bernoulli): 8자 또는 무한대 기호와 같은 곡선
5. 카시니 타원(Cassinian Ovals): 두 고정점에서의 거리 곱이 일정한 곡선
6. 니코메데스의 콘코이드(Conchoid of Nicomedes): 고정점에서 선까지의 거리에 따라 형태가 결정되는 곡선
7. 데카르트의 폴리움(Folium of Descartes): 흥미로운 루프를 형성하는 함수
8. 사이클로이드(Cycloid): 직선을 따라 굴러가는 원의 둘레 위의 점이 그리는 곡선
9. 에피사이클로이드(Epicycloid): 다른 고정 원의 외부를 따라 굴러가는 원의 둘레 위의 점이 그리는 곡선
10. 하이포사이클로이드(Hypocycloid): 다른 고정 원의 내부를 따라 굴러가는 원의 둘레 위의 점이 그리는 곡선
11. 원의 인볼루트(Involute of a Circle): 원에서 팽팽한 줄이 풀리면서 줄 끝이 그리는 곡선
12. 만델브로트 집합(Mandelbrot Set): 복소 평면에서 간단한 이차 방정식을 반복적으로 적용하여 생성되는 유명하고 무한히 복잡한 프랙탈
13. 줄리아 집합(Julia Sets): 만델브로트 집합과 밀접하게 관련된 프랙탈 가족
14. 뉴턴 프랙탈(Newton Fractals): 다항식에 적용된 뉴턴 방법에 의해 결정되는 복소 평면의 경계
15. 반슬리 고사리(Barnsley Fern): 반복 함수 시스템에 의해 생성되는 고사리와 비슷한 프랙탈

또한 프롬프트에 무드보드를 추가하여 추가적인 스타일과 외관을 부여했습니다. 이것이 사실 과정에서 가장 재미있는 부분입니다: 우아하고 독특하며 미학적으로 즐거운 무언가를 만드는 스타일의 조합을 찾는 것입니다.

미드저니 V7의 성능 평가

미드저니는 수학적 아트 생성을 감각적으로 잘 표현합니다.. 우아한 선과 형태를 특징으로 하는 멋진 이미지들을 많이 만들어냈으며, 이는 시선과 관심을 사로잡는 – 좋은 이미지가 달성해야 할 모든 것을 잘 표현해주고 있습니다

실제 예시: 만델브로트 집합(Mandelbrot Set)

프롬프트: Abstract mathematical art, Mandelbrot Set, shallow focus, bokeh, vibrant colors, high contrast

이 프롬프트로 만든 이미지는 만델브로트 집합의 특징적인 나선형 구조와 프랙탈 패턴을 보여줍니다. 무한히 확대해도 유사한 패턴이 반복되는 만델브로트 집합의 성질이 미드저니 V7에서 아름답게 표현되었습니다. 이미지는 중앙 부분에 짙은 검정색 영역이 있고, 가장자리로 갈수록 파란색, 보라색, 분홍색 등의 화려한 색상이 번져 나갑니다. 얕은 초점 기법과 보케 효과가 더해져 마치 우주의 신비로운 한 구석을 들여다보는 듯한 느낌을 줍니다.

실제 예시: 줄리아 집합(Julia Set)

프롬프트: Abstract mathematical art, Julia Set, shallow focus, bokeh, neon colors, dark background

줄리아 집합은 만델브로트 집합과 수학적으로 관련이 있지만, 다른 형태의 아름다움을 보여줍니다. 미드저니 V7로 만든 이미지에서는 어두운 배경에 네온 색상의 나선형 패턴이 마치 발광하는 것처럼 표현되었습니다. 중심부에서는 세밀한 구조가 명확히 보이고, 바깥쪽으로 갈수록 흐릿해지는 보케 효과가 적용되어 몽환적인 분위기를 자아냅니다. 수학적 정확성보다는 예술적 해석에 가깝지만, 줄리아 집합의 본질적인 아름다움을 잘 포착하고 있습니다.

실제 예시: 벤 다이어그램(Venn Diagram)

프롬프트: Abstract mathematical art, Venn Diagram, shallow focus, bokeh, minimalist, pastel colors

일반적으로 데이터 시각화에 사용되는 벤 다이어그램을 미드저니 V7은 예술적으로 재해석했습니다. 이 이미지에서는 서로 겹치는 원형 구조가 파스텔 색상으로 표현되었고, 겹치는 부분에서는 색상이 혼합되며 아름다운 그라데이션을 형성합니다. 미니멀리스트 접근 방식으로 불필요한 요소를 제거하고 순수한 기하학적 형태에 집중했습니다. 얕은 초점 덕분에 일부 영역은 선명하게, 다른 영역은 부드럽게 흐려져 공간감을 더했습니다.

수학 이미지에 대한 저자의 매력은 수학에 대해 따뜻한 감정을 갖지 않는 대부분의 사람들에게는 약간 이상하게 들릴 수 있습니다. 하지만 간단한 진실은 다음과 같습니다: 저자는 다른 모든 스타일과 예술 형태의 이미지를 합친 것보다 더 많은 수학 기반 이미지를 판매했습니다.

수학적 아트의 실용적 활용

추상적인 수학 아트는 다음과 같은 용도로 탁월합니다:

• 벽 장식용 예술품
• 데스크톱 배경화면
• 수학 아트 마우스패드

특히 컴퓨터로 작업하는 사람들은 마우스 아래의 우아한 수학적 디자인을 감상합니다.

실제 활용 예시: 프랙탈 아트 인테리어

프롬프트: Abstract mathematical art, Fractal, shallow focus, interior design, modern living room, framed art

한 현대적인 거실 인테리어에 프랙탈 아트를 활용한 예시입니다. 미니멀한 화이트 톤 거실의 소파 위에 걸린 대형 프랙탈 아트 작품은 공간의 초점이 됩니다. 선명한 파랑, 보라, 초록색의 복잡한 패턴이 화이트 인테리어와 극명한 대비를 이루며 공간에 활기를 불어넣습니다. 이 작품은 단순히 장식적인 요소를 넘어 지적 호기심을 자극하는 대화의 주제가 됩니다.

실제 활용 예시: 수학 아트 기업 브랜딩

프롬프트: Abstract mathematical art, Euler Diagram, shallow focus, business card design, corporate identity, minimalist

한 기술 기업이 오일러 다이어그램을 활용한 브랜딩을 선보였습니다. 명함에는 겹치는 원형의 세련된 기하학적 패턴이 은은한 메탈릭 마감으로 인쇄되어 있습니다. 이 디자인은 회사의 웹사이트, 제품 패키지, 사무실 인테리어 등에 일관되게 적용되어 수학적 정확성과 혁신을 중시하는 기업 이미지를 강화합니다. 단순하지만 의미 있는 이 수학적 아트는 기업의 정체성을 효과적으로 전달합니다.

마치며

미드저니 V7 알파의 기본 원리와 수학 기반 아트를 만드는 능력을 보여주는 몇 가지 예시를 이 글에 포함했습니다. 하지만 앞서 언급했듯이, 여러분만의 개인화, 무드보드, 스타일 참조를 통해 가능성은 무한합니다.

성공적인 수학 아트 프로젝트 사례

프롬프트: Abstract mathematical art, Barnsley Fern, shallow focus, bokeh, product design, eco-friendly packaging

한 유기농 식품 브랜드는 반슬리 고사리 프랙탈을 활용한 패키지 디자인으로 주목을 받았습니다. 이 디자인은 미드저니 V7로 생성한 초록색 톤의 고사리 패턴을 재활용 종이에 인쇄했습니다. 수학적으로 생성된 고사리 패턴은 자연스러우면서도 정교한 느낌을 주어 유기농 제품의 천연 이미지와 완벽하게 조화를 이룹니다. 이 브랜드는 수학적 아트를 활용한 독특한 디자인으로 경쟁사와 차별화에 성공했으며 판매량이 32% 증가했다고 보고했습니다.

일상에서 만나는 수학 아트

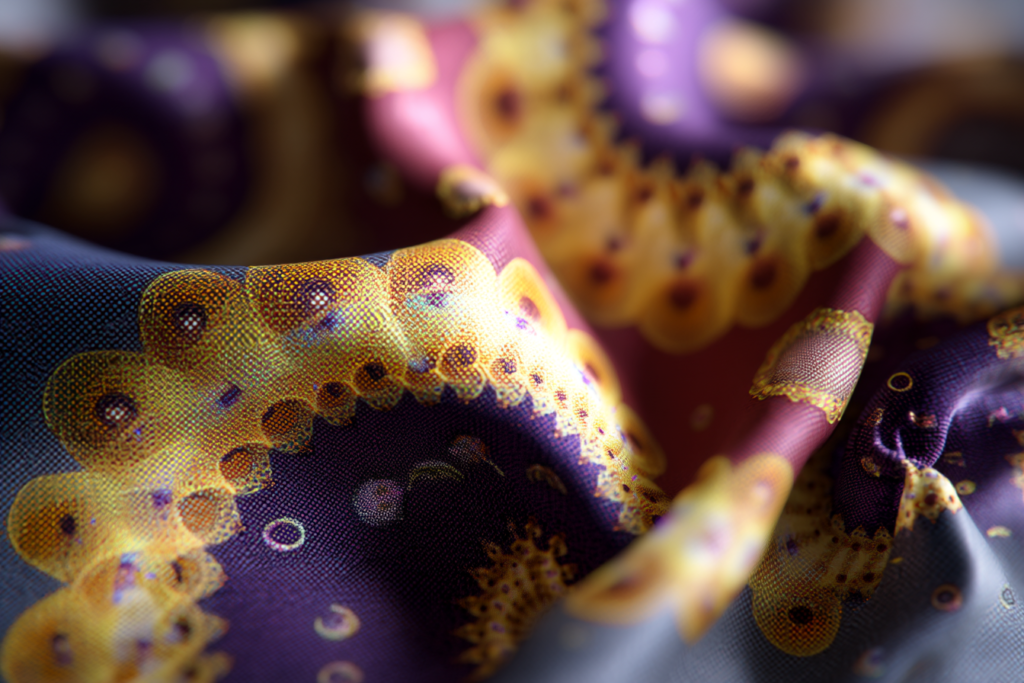
프롬프트: Abstract mathematical art, Hypocycloid, shallow focus, bokeh, fashion design, silk scarf pattern

패션 디자이너들 사이에서도 수학적 패턴을 활용한 디자인이 트렌드로 자리 잡고 있습니다. 특히 하이포사이클로이드 패턴을 실크 스카프에 적용한 디자인은 세련된 기하학적 아름다움으로 많은 사랑을 받고 있습니다. 곡선이 그리는 대칭적인 패턴은 다양한 스타일링에 어울리며, 멀리서 보면 단순한 패턴처럼 보이지만 가까이서 보면 복잡한 수학적 구조를 감상할 수 있다는 점이 매력적입니다.

여러분도 최소한 미드저니를 통해 수학적 아트를 시도해보길 권장합니다. 의외로 매력적인 결과물을 얻을 수 있을 것입니다.

수학적 아트를 시작하기 위한 팁

미드저니를 사용해 수학적 아트를 만들고 싶다면 다음 팁을 참고하세요:

1. 간단한 함수부터 시작하기: 벤 다이어그램이나 줄리아 집합처럼 시각적으로 인식하기 쉬운 함수부터 시작해보세요.
2. 프롬프트 실험하기: “Abstract mathematical art”를 기본으로 하되, 다양한 수식어를 추가해보세요.
3. 무드보드 활용하기: 원하는 색상 팔레트나 스타일을 가진 이미지를 참조 이미지로 추가하면 더 원하는 결과를 얻을 수 있습니다.
4. 다양한 렌더링 스타일 시도하기: “shallow focus”, “bokeh” 외에도 “neon”, “holographic”, “paper art” 등 다양한 스타일을 시도해보세요.
5. 해상도와 비율 조절하기: 특정 함수는 특정 이미지 비율에서 더 잘 표현될 수 있습니다.

초보자를 위한 단계별 튜토리얼

프롬프트: Abstract mathematical art, Lemniscate of Bernoulli, shallow focus, bokeh, colorful gradient, simple

베르누이의 렘니스케이트(무한대 기호 모양 곡선)로 첫 수학적 아트를 만들어보세요. 이 간단한 함수는 시각적으로 친숙하면서도 아름다운 결과물을 만들어냅니다.

1. 미드저니에 위 프롬프트를 입력합니다.
2. 생성된 이미지 중 마음에 드는 것을 선택합니다.
3. 색상이나 스타일을 변경하고 싶다면 “colorful gradient” 부분을 “blue to purple gradient” 또는 “metallic gold” 등으로 바꿔보세요.
4. 렌더링 스타일을 바꾸고 싶다면 “bokeh” 부분을 “holographic”, “glowing”, “3D render” 등으로 변경해보세요.

이렇게 만든 첫 번째 이미지는 무한대 기호를 기본으로 하지만 예술적으로 재해석되어 부드러운 그라데이션과 초점 효과가 더해진 아름다운 추상 이미지가 됩니다.

고급 사용자를 위한 테크닉

프롬프트: Abstract mathematical art, Newton Fractal, shallow focus, bokeh, dark background, highly detailed, intricate patterns, iridescent colors 

경험이 쌓이면 더 복잡한 함수와 고급 설정을 시도해볼 수 있습니다. 뉴턴 프랙탈은 복잡한 패턴을 만들어내며, 위의 프롬프트에서는 이리데센트(무지개빛) 색상을 어두운 배경에 대비시켜 드라마틱한 효과를 줍니다. 또한 16:9 비율과 높은 품질 설정으로 더 자세하고 영화적인 이미지를 만들어냅니다.

수학적 아트는 단순한 시각적 즐거움을 넘어 깊은 개념적 의미를 담고 있습니다. 미드저니 V7은 이러한 추상적 개념을 더욱 아름답게 표현할 수 있게 해주는 강력한 도구입니다. 여러분만의 수학적 예술 작품을 만들어보세요!